SLR + MLR

Lecture 13

Dr. Elijah Meyer

Duke University
STA 199 - Spring 2023

Feburary 24th, 2023

Checklist

– Clone `ae-12

– Homework 2 due tonight (11:59)

– Lab 4 due Tuesday (11:59)

— 1 submission. Attach everyone to it

Data Fest 2023 at Duke

– data analysis competition where teams of up to five students attack a large, complex, and surprise dataset over a weekend

– DataFest is a great opportunity to gain experience that employers are looking for

– Each team will give a brief presentation of their findings that will be judged by a panel of judges comprised of faculty and professionals from a variety of fields.

Lab 4

– Team Submission

– Attach ALL team members to submission on Gradescope

– Communicate!

– “It was my responsibility to turn the lab in and I forgot….”

Goals

– Discuss correlation

– Finish categorical single predictor

– Model with multiple predictors

Warm up

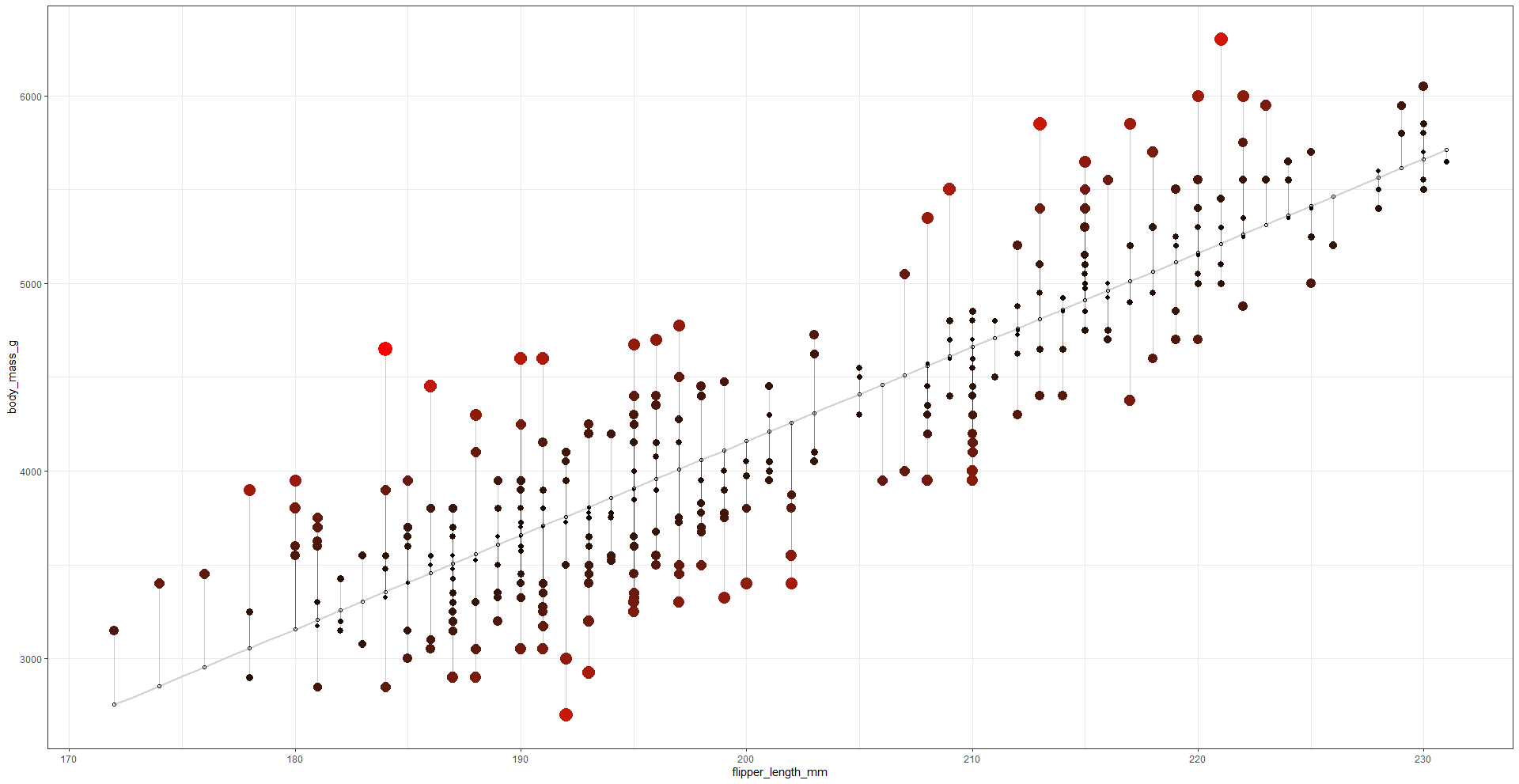
Below is a scatterplot from ae-11. Alone or with a partner, discuss how R chose to fit this line over any other.

Warm up

Correlation

– Proper notation:

— Population correlation: \(\rho\)

— r

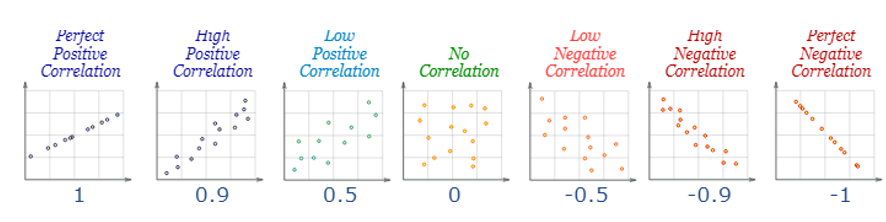
Correlation

strength and direction of a linear relationship

bounded between [-1, 1]

The Correlation Game

– Play against yourself

– Be better at correlation than your friends

https://www.rossmanchance.com/applets/2021/guesscorrelation/GuessCorrelation.html

Correlation

Can find this with the cor or correlate function in R

https://www.tidyverse.org/blog/2020/12/corrr-0-4-3/

Models

Single Predictor - Categorical Variable

ae-12

Multiple Linear Regression

estimates the relationship between a quantitative response variable and two or more explanatory variables

motivated by scenarios where many variables may be simultaneously connected to an output

Multiple Linear Regression

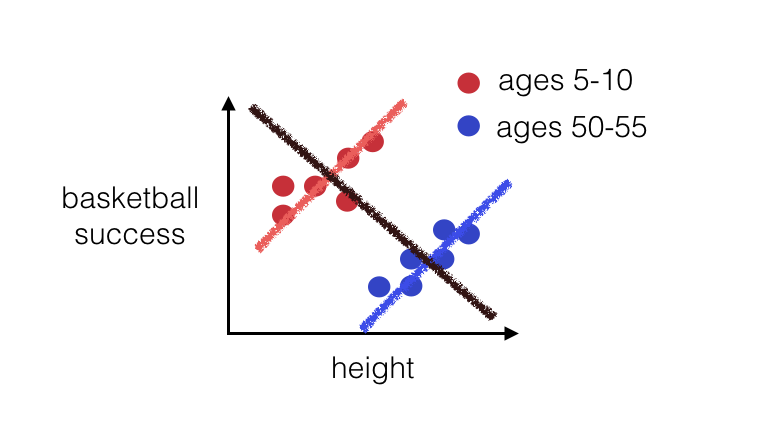
Additive Model vs Interaction Model

In words….

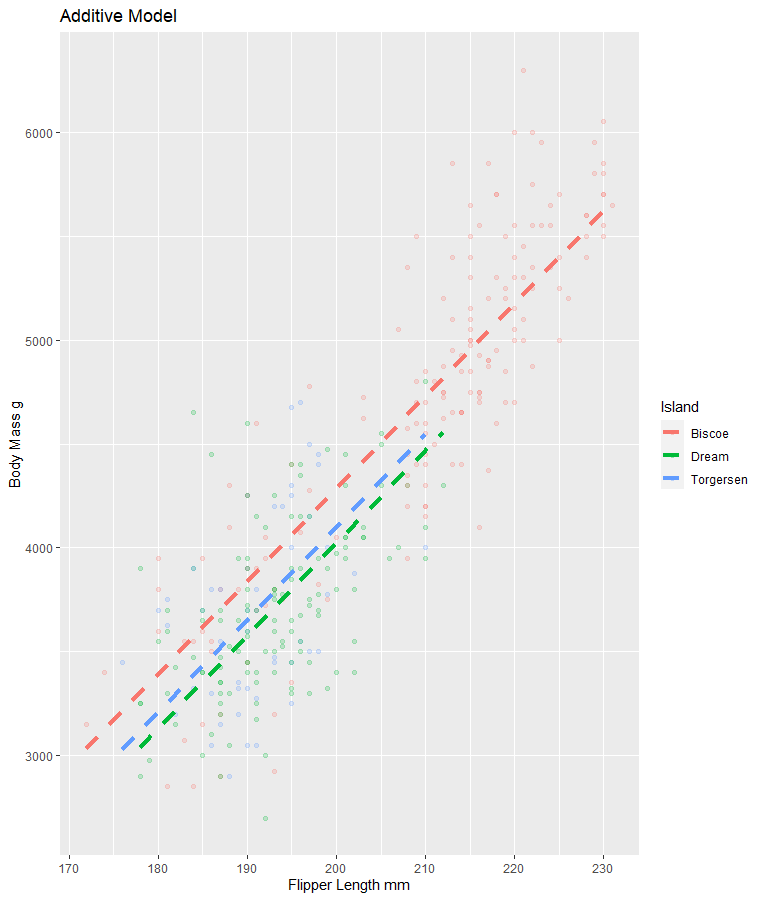
The relationship between x and y do not change based on the values of z (additive)

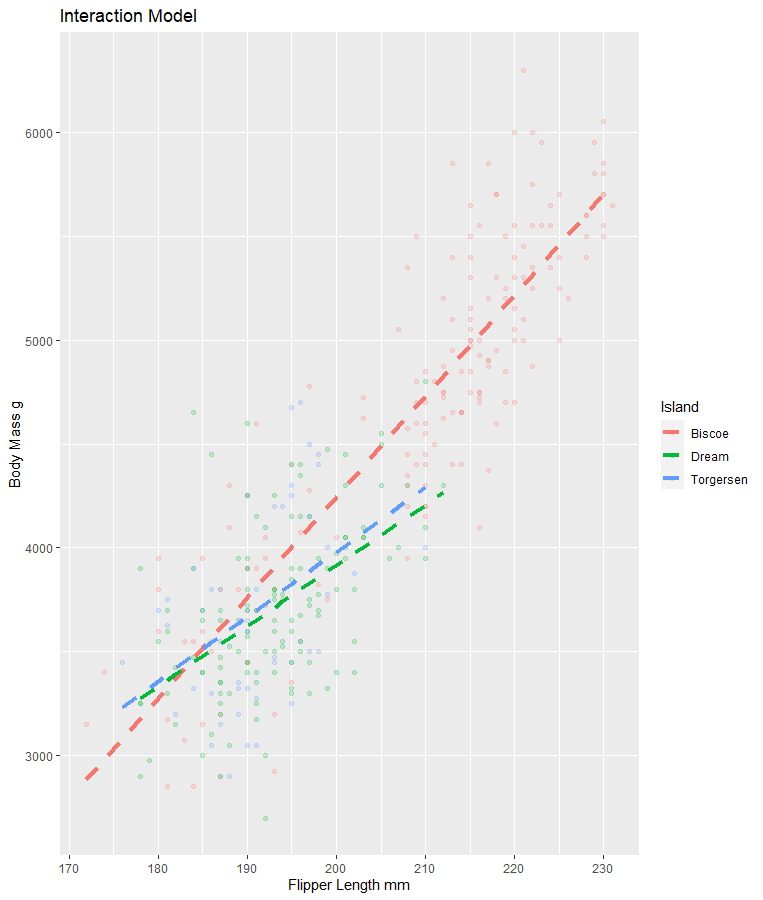
The relationship between x and y DO change based on the values of z (interaction)

Additive Model for Today

Interaction Model for Today

Principle of parsimony (Occam’s Razor)

for a statistical model states that: a simpler model with fewer parameters is favored over more complex models with more parameters, provided the models fit the data similarly well

KEEP IT SIMPLE (when you can)

So how do we choose?

Many different ways

– Initial visual evidence

– R-squared & Adjusted R-squared

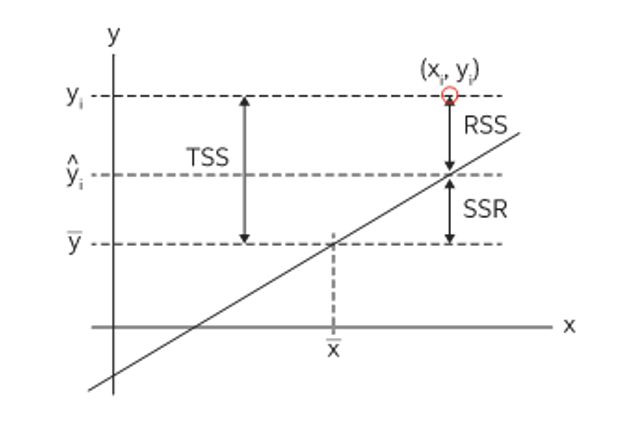
R-squared

– statistical measure in a regression model that determines the proportion of variance in the response variable that can be explained by the explanatory variable(s).

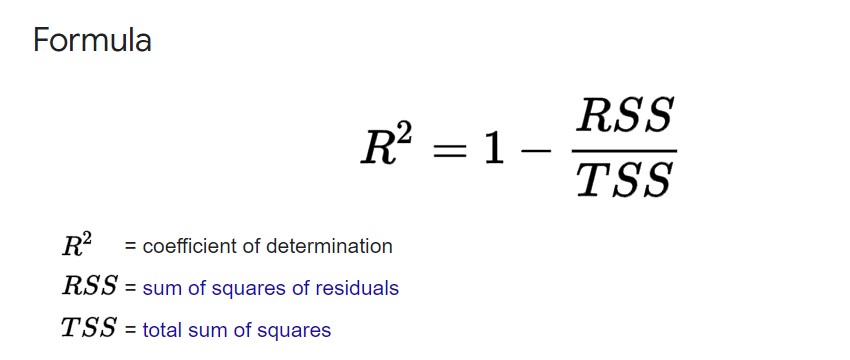
R-squared

R-squared: Takeaway

– statistical measure in a regression model that determines the proportion of variance in the response variable that can be explained by the explanatory variable(s).

– The more variables you include, the larger the R-squared value will be (always)

Adjusted R-squared

Takeaway: Adds a penalty for “unimportant” predictors (x’s)