Conditional Probability

Lecture 11

Dr. Elijah Meyer

Duke University
STA 199 - Spring 2023

February 17th, 2023

Checklist

– Clone ae-10

– HW-2 coming shortly after class (due 1-week)

– Groups public soon after class

– team repos for lab

Announcements

– Do not start lab-4 early

– Gradescope vs Gradebook

Goals

Exploring Relationships of data

be able to define and compute marginal, joint and conditional probabilities
Fill in contingency tables
identify when events are independent
Have an understanding of Bayes’ theorem
Simpson’s Paradox

Last Time

– Terms

Event
Sample Space

Last Time: Types of probabilities

– Single Event

– “And”

– “Or”

Same Concept - Different Names

– Single Event : Marginal Probability

– “And” : Joint Probability

– “Or” : Joint Probability

Same Concept - Different Terms

– P(A and B) = P(A \(\cap\) B)

– P(A or B) = P(A \(\cup\) B)

Quick Example

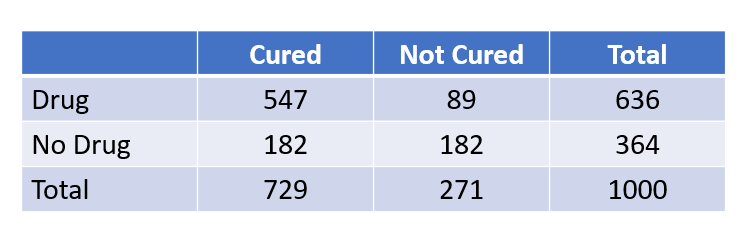
Let A represent being cured from the disease

Let B represent taking the drug

What’s the sample space for A?
P(A) =
P(A and B) =
P(A or B) =

Conditional Probability

– formally, we define conditional probability as P(A|B)

– “|” represents “given”

Example

Let A represent being cured from the disease

Let B represent taking the drug

– P(B|A) =

Helpful rules: Bayes Theorem

– is a mathematical formula used to determine the conditional probability of events.

– describes the probability of an event based on prior knowledge of the conditions that might be relevant to the event

– P(A|B) = \(\frac{P(B|A) * P(A)}{P(B)}\)

In action

Let A represent being cured from the disease

Let B represent taking the drug

P(A|B) = \(\frac{P(B|A) * P(A)}{P(B)}\)

Helpful rules: Law of total probability

– the probability that A occurs is equal to the sum of the probabilities that A occurs with B and that A occurs without B

– P(A) = P(A and B) + P(A and \(B^c\))

Helpful rules: Independence

– P(A|B) = P(A)

Independence

Let A represent being cured from the disease

Let B represent taking the drug

– Are A and B independent?

ae-10

Simpson’s Paradox

– is a statistical phenomenon where an association between two variables in a population emerges, disappears or reverses when the population is divided into subpopulations

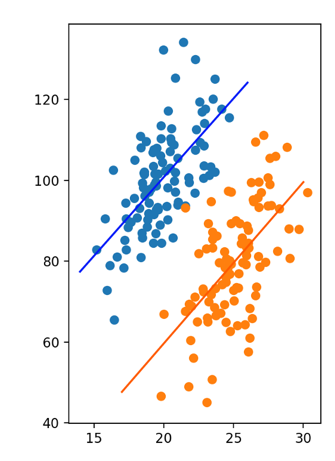
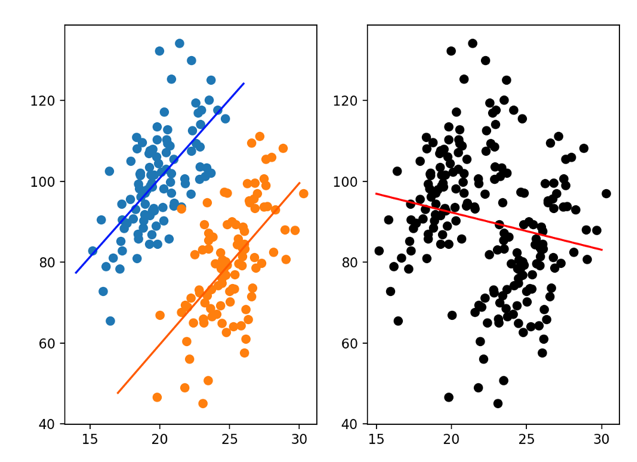
Simpson’s Paradox